理論:交流回路:力率、直列・並列回路



解説
今まで出てきた中では一番難しい問題。直列回路と並列回路が一緒になっているので、ベクトル図を描いて順序立てて考えることが必須。
誘導性負荷:
インピーダンスが全体で遅れになっている負荷のこと。L だけが含まれる回路のことではなく、L とC 両方があっても電流の位相が遅れになっていれば誘導性という。なのでノートに描いた r と L の直列回路はあくまでモデルで、C がある場合もあり得る。力率0.6 という条件は定番。cosθ=0.6 ↔︎ sinθ=0.8。三角形の比は3:4:5。
まず並列回路を誘導性負荷と抵抗負荷Rに切り分けて考える。Rに流れる電流IR は電圧Eと同相。
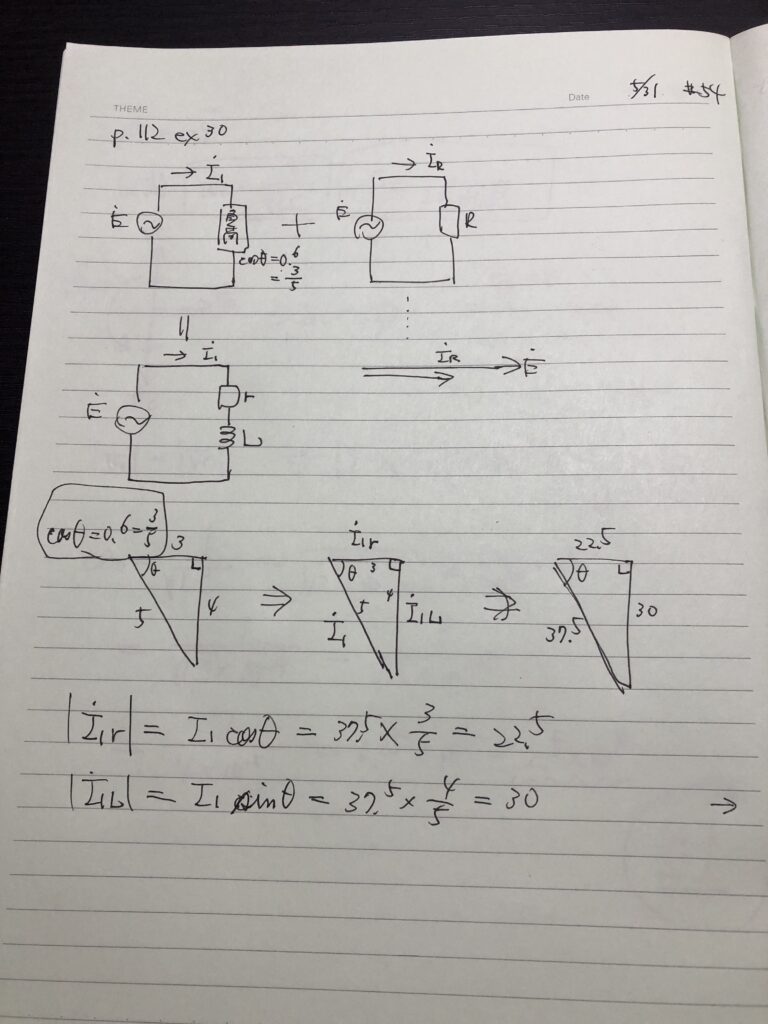
誘導性負荷は力率0.6で3:4:5の三角形なので、流れる電流I1 =37.5 からI1r とI1L を得られる。しかし「I1r 」「I1L 」とは何か?
ここが一番難しいところで、電流をベクトル分解して電圧と同相の成分と90° 遅れの成分に分けている。でも何で直列回路の電流を2つの位相に分解できるのか?
- 直列回路では電流は共通だから位相は一つだけじゃないの? →その通り
- 直列回路では電流を基準にして電圧のベクトルを考えるんじゃないの? →ここではそうしない
この問題は全体としては並列回路。並列回路では全体にかかる電圧を基準にして、各枝に流れる電流の位相と大きさを求めていくのが基本。なので直列になっている枝でも電流に着目していく。そして誘導性負荷に流れる「遅れ」電流を「90° 遅れている要素」と「遅れていない(電圧と同相)要素」の2つから構成されていると考える。(無理やり?)
ちゃんと理解しておらずうまく説明できない。次↓の目的のためにこうする、としか言えない。
なぜ位相別に要素を分解するのか? 最終的に同じ位相ごとに大きさを計算するため。ノート2ページ目のように、誘導性負荷の回路とRの回路のベクトル図を合成する。ここで位相が同じ矢印を加算する。電圧と同相の2つの要素「IR +I1r 」と90° 遅れ要素「I1L 」から回路全体の電流「I」の三角形ができる。
この三角形も3:4:5になっている。なので大きさは図から「IR +I1r 」=40 とわかる。(ノートの大きさの式は使わなくていい)


コメント