理論:静電気:コンデンサ、比誘電率、直列接続
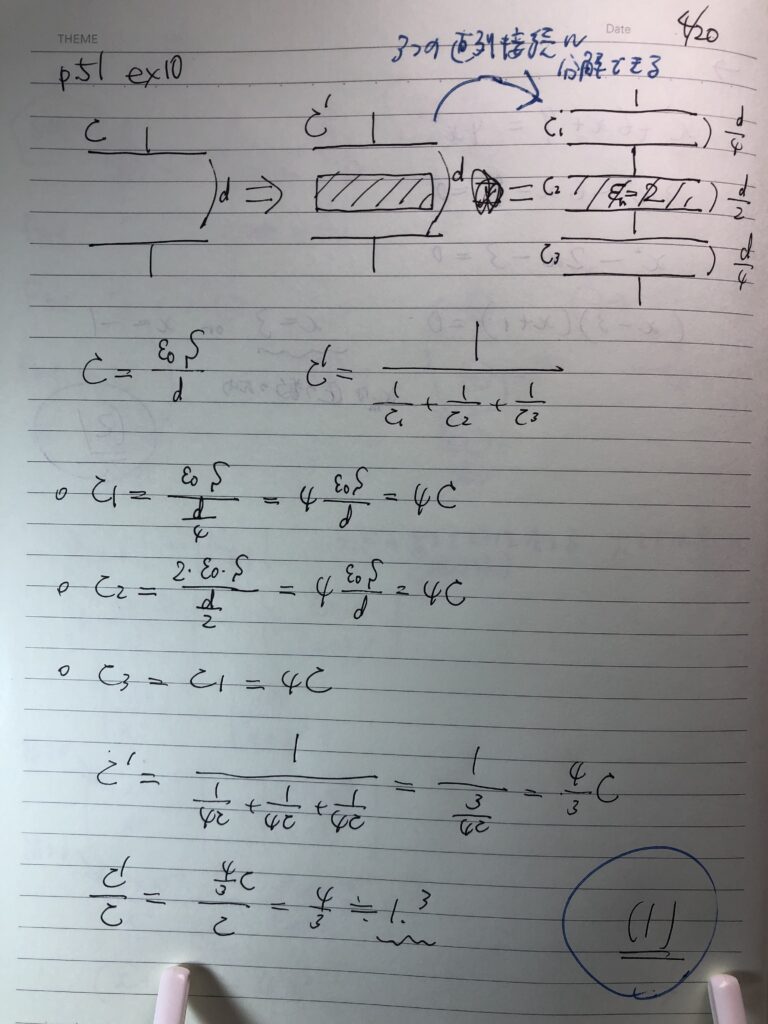
解説
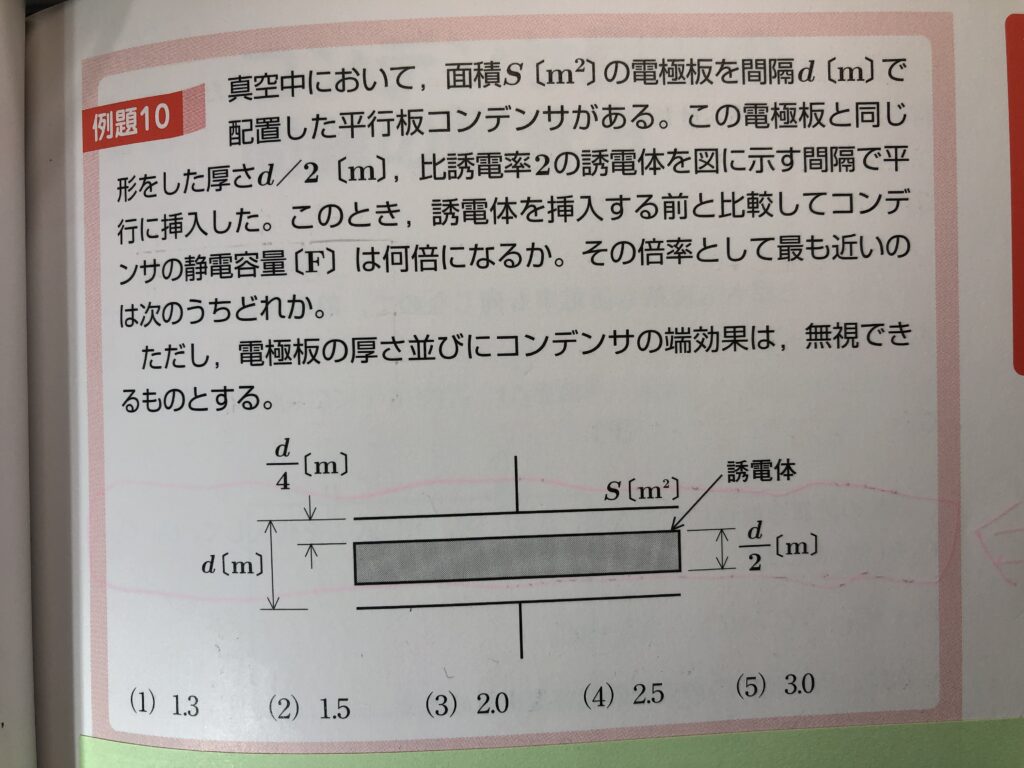
こういった誘電体を挿入する形の問題は多いが解き方は決まっている。
まず、誘電体を挿入する前の「素の」コンデンサ容量の式を立てる。(公式 C=ε0*S/d)次に、誘電体を挿入したら3つのコンデンサに分割し直列接続として考える。それぞれのコンデンサについて、同様に容量Cnの式を立てる。この時、比誘電率εnと間隔dを変えて代入する。
【ポイント】個々のコンデンサの式を、挿入前のCの何倍か、の式に変換する。
この手の問題はほとんどが比率を問う問題なので「挿入前の何倍(何分の1)」の形にすぐ変換する。ε、d、Sの式のまま計算してはいけない。
倍率の形にしたら、倍率のまま直列合成して挿入前と比較するだけ。
補足
今回は問題の形に合わせて3つのコンデンサに分割して解いたが、3つの直列の式は煩雑なので通常は2つのコンデンサに集約して考える。挿入された誘電体は移動して考えてもいいので、下図↓のように上または下に移動して、真空部分を合体させて2つのコンデンサにすれば直列の計算がしやすい。



コメント